MATLAB codes for Blind compressed sensing (BCS) dynamic MRI

1. Motivation:

• BCS models the dynamic time profile at every voxel as a sparse linear combination of learned temporal basis functions from a dictionary. The basis functions and the spatial weights/model coefficients are jointly estimated from the undersampled measurements. 

• The main motivation of using learned basis functions is that the bases are more representative of the temporal dynamics at hand and adapt to the data; they provide sparser representation compared to off the shelf dictionary bases (eg:  Fourier exponential bases) as used in conventional compressed sensing. Further in dynamic MRI since the number of voxels per frame typically dominate the number of time frames, the overhead in learning the basis functions is minimal. This is demonstrated in the example phase transition plot (click here ) of compressed sensing with fixed Fourier bases v/s blind CS with learned bases from undersampled data v/s a setting where the ideal dictionary bases are known.

• BCS contrasts with low rank based methods that utilize few orthogonal temporal bases which have degrees of freedom proportional to the rank of the model ; the key difference is (a) the sparsity of the BCS model coefficients and (b) the increased number of non-orthogonal basis functions in the dictionary which provides a richer representation. In contrast to low rank models, the degrees of freedom of the BCS model is proportional to the sparsity level. Click here for a pictorial comparison of the degrees of freedom of the low rank and BCS models.

2. Blind CS formulations:

• Version 1.1 Penalty based formulation (Single Coil) [Download the codes here]

• We pose the simultaneous estimation of the model coefficients (U_MxR) and the dictionary matrix (V_RxN) as the following optimization problem:  

• Here, M, N, R are respectively the number of voxels per frame, the total number of time frames, and the number of basis functions in the dictionary. The l₁ norm prior is used on the coefficient matrix to promote sparsity, while the energy preserving Frobenius norm is used on the dictionary to make the problem well posed. A is the Fourier sampling operator; the example codess provided in Version 1.1 are based on single coil data. The free regularization parameters lambda1 and lambda2 should be optimized accordingly for best results. This formulation was used in references [i,ii,iii,iv] below.

• Version 2.1 : Constraint based formulation [Download codes here] Ref [v, vi]

• We generalize the previous version to include non-convex l_p norm (p<1) priors on U, generalized constraints on V (eg: Frobenius norm, unit column norm, l₁-l₂ norm constraints), and also leverage information from multiple coils (parallel imaging) [Used in reference [v, vi] below]:     

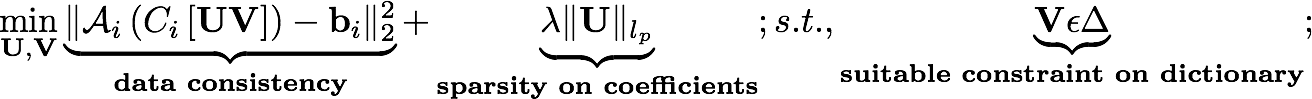
• Version 2.2 : Fast BCS implementation [Download codes here] Ref [vi]

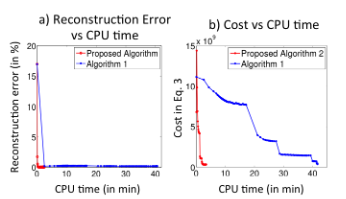
• We propose a optimization algorithm that utilizes variable splitting strategies to significantly improve the convergence speed of the BCS optimization. The splitting allows us to efficiently decouple the sparse coefficient, and dictionary update steps from the data fidelity term, resulting in subproblems that take closed form analytical solutions, which otherwise require slower iterative conjugate gradient algorithms. [Used in reference [vi].

3. Examples provided: [version 1.1]

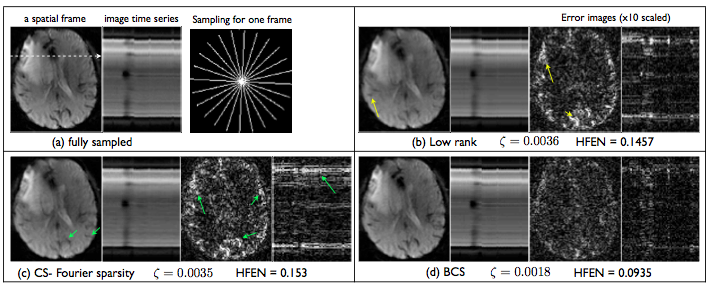
•  Run main_run_brain.m to replicate the below result on a brain perfusion MRI dataset

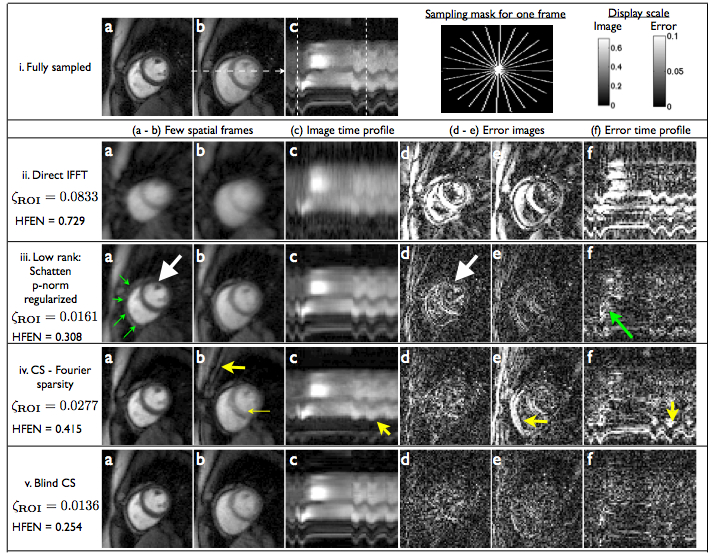
•  Run main_run_cardiac.m to replicate the below result on a myocardial perfusion MRI dataset

\

• Run main.m to replicate the below result

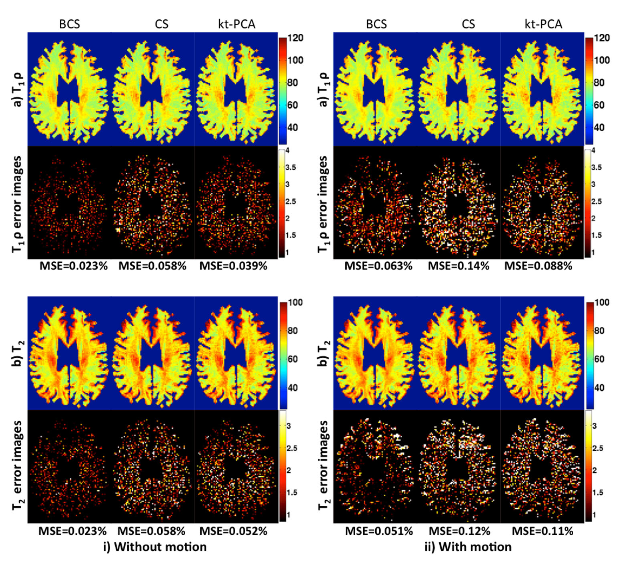
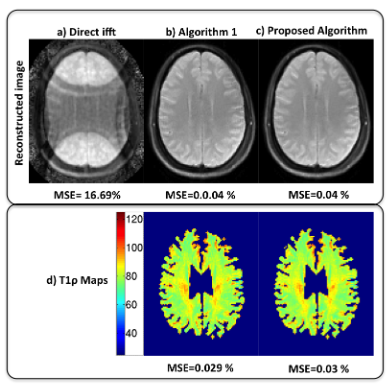
• Run main_fastbcs.m to replicate the result below