Patch-based Shrinkage Regularization
Download Matlab Code: Code
Installation: The above link will get you to the code folder, simply uncompress the folder and run the demo function mainpublish.m. This code will replicate the results reported in the TMI and EMBC papers.
Framework: We present a fast iterative shrinkage algorithm for patch-smoothness regularization to recover medical imaging. The proposed algorithm alternates between evaluating the denoised inter-patch differences by shrinkage and computing an image that is consistent with the denoised inter-patch differences and measured data. We derive analytical shrinkage rules for several penalties that are relevant in non-local regularization. The redundancy in patch comparisons used to evaluate the shrinkage steps are exploited using convolution operations. The resulting algorithm is observed to be considerably faster than current alternating non-local algorithms. The proposed scheme is applicable to a large class of inverse problems including deblurring, denoising, and Fourier inversion. The comparisons of the proposed scheme with state of the art regularization schemes in the context of recovering images from undersampled Fourier measurements demonstrate a considerable reduction in alias artifacts and preservation of edges.
llustration:
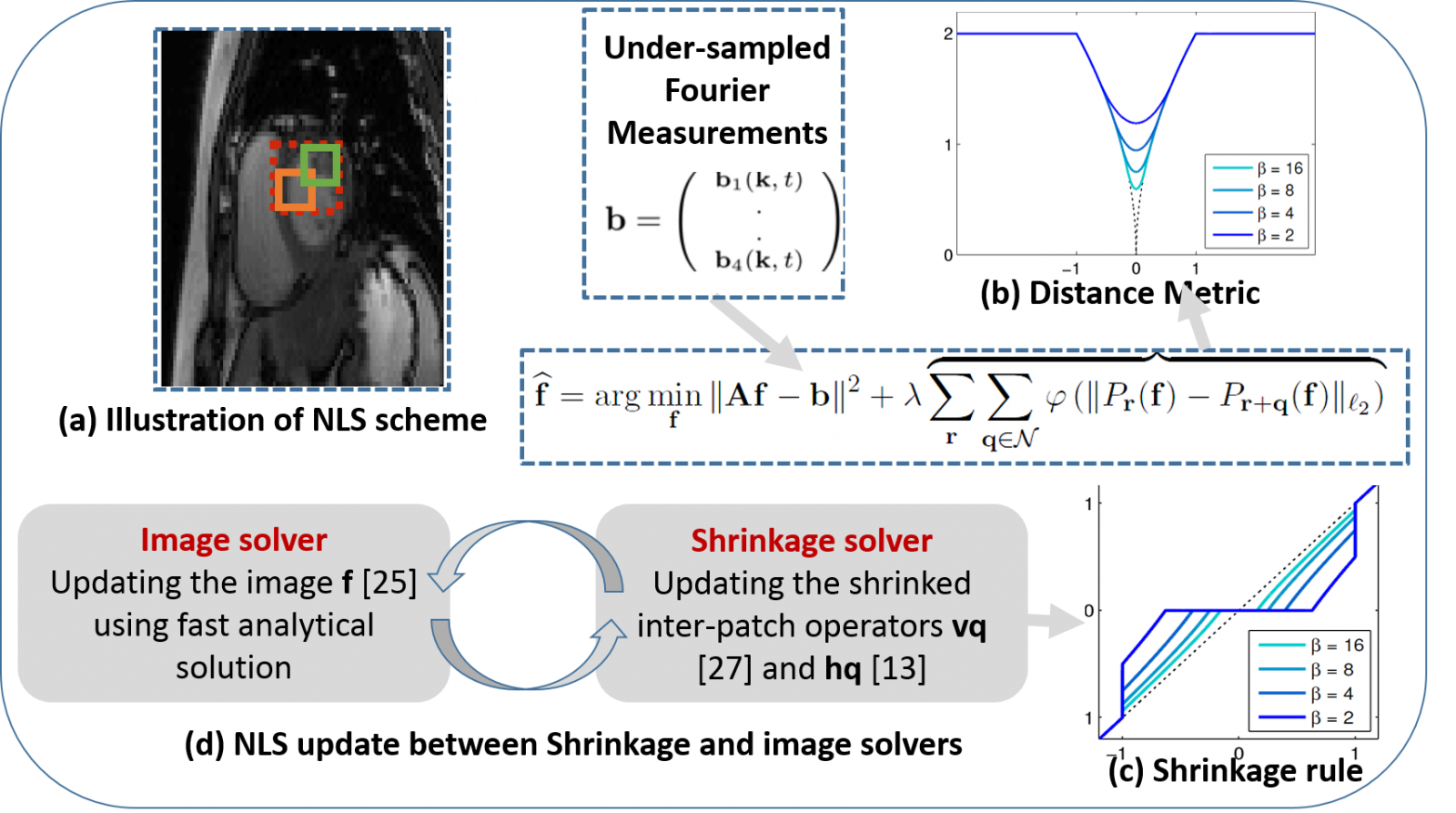
Illustration of the proposed scheme. The regularization term penalizes the differences between each patch and other patches in its neighborhood. The green and orange squares indicate the location of the patches with the highest similarity in the neighborhood. The dashed red box represents the neighborhood where the patches move within. The distance metric used for the comparison is shown by the dotted black curve in (b). The metric heavily penalizes the distances between similar patches, while it eliminates dissimilar patches from the comparison; this minimizes the spatial blurring induced by the averaging of dissimilar patches. The colored curves correspond to the different approximations of the distance metric, which enables fast algorithms. (c) The shrinkage rule for the inter-patch differences using Lp. We rely on continuation schemes as shown in (b) and (c) starting with low values of Beta and gradually increase it to high values, when the approximation is more accurate. (d) The algorithm alternates between a simple shrinkage step to denoise inter patch differences and image update step, which involves a computationally efficient anaytical solution.
Comaprison:
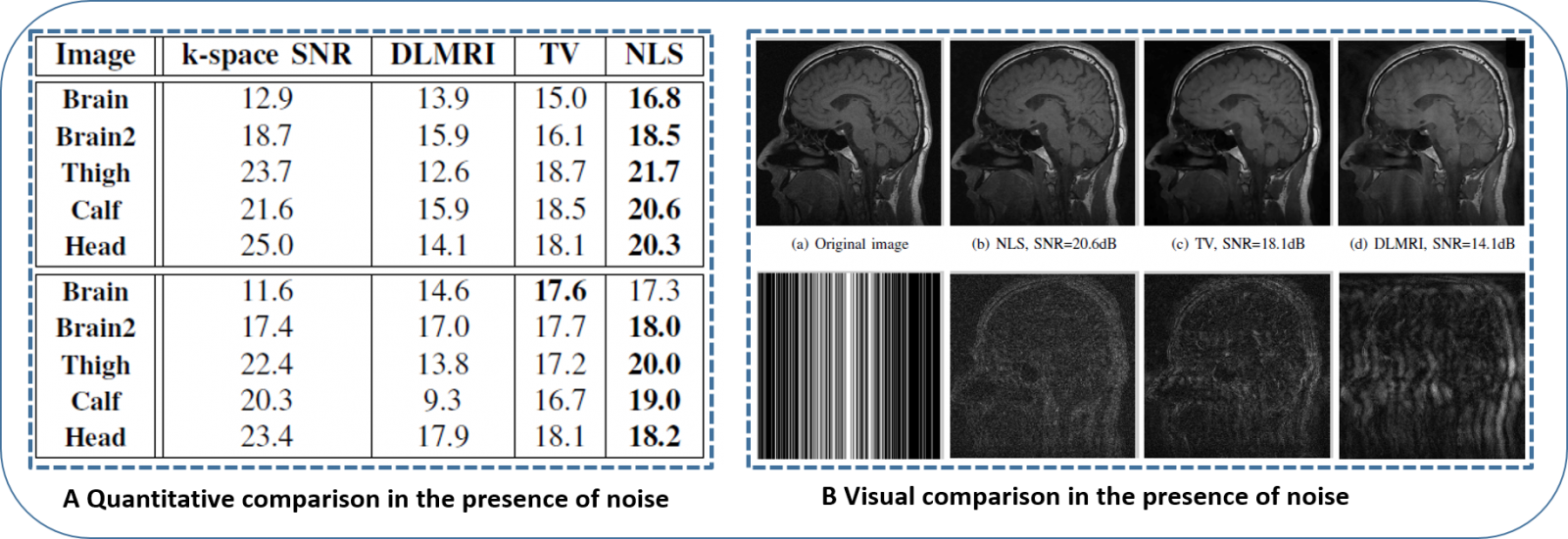
References:
-
Y. Mohsin, G. Ongie, M. Jacob "Iterative shrinkage algorithm for patch smoothness regularized medical image recovery, IEEE TMI,2015. -
Z. Yang, M. Jacob,"Nonlocal regularization of inverse problems: a unified variational framework", IEEE TIP, pp: 3192-203, vol.22(8), Aug 2013.
-
Y. Mohsin, G. Ongie, M. Jacob, "Accelerated MRI using iterative non-local shrinkage", IEEE EMBC, Chicago, USA, 2014.
-
Z.Yang, M. Jacob,"A unified energy minimization framework for nonlocal regularization", IEEE ISBI, Chicago", April 2011.
- Log in to post comments
